Stable multivariate lesion symptom mapping

Introduction

Lesion mapping is central to theories of functional neuroanatomy.¹ Seminal case studies from the 19^th century relating lesion location to behavioral deficits have considerably shaped modern understanding of brain function.^2,3 The principle that location of brain damage can reveal causal information about where cognitive processes are implemented in the brain continues to be productive for cognitive neuroscience and there is a growing number of studies leveraging lesion-symptom mapping (LSM) methods.^4–6

Unlike older lesion mapping approaches that evaluated the locus of lesion overlap, modern LSM studies employ more sophisticated statistical analyses to objectively identify voxels that are consistently damaged in individuals with a specific impairment yet spared in those without the symptom.⁷ Traditional LSM is conducted using a mass-univariate approach in which damage to each voxel (or region) of the brain is independently tested for its association with a given impairment. This approach generates some inferential challenges. A more comprehensive review of these may be found elsewhere.^6,8–12 Here, we briefly consider how multivariate methods can capture unique patterns of brain damage that address some of the inferential limitations of LSM, describe how the conventional multivariate lesion-symptom mapping (MLSM) pipeline functions, and motivate a modification that can mitigate some of MLSM’s shortcomings.

1. Identifying more complex patterns of damage with multivariate lesion symptom mapping

The assumption in LSM that deficits stem from damage to isolated regions of the brain oversimplifies the complexity of brain injury. Consider an impairment that is observed when either of two brain regions is injured (e.g., a sequential processing network as seen in the primary sensory cortices). In this situation, a mass univariate approach has very little statistical power, as damage restricted to one node provides a counterexample for the criticality of the other. Here LSM may struggle to identify the relevancy of either region. Alternatively, consider a situation where the brain has some redundancy, where a symptom is only seen when two regions are both injured. Again, apparent counterexamples lead to low statistical power.

Multivariate methods can leverage the pattern of damage across the brain synergistically to predict behavior, capturing more complex damage to explain impairments.¹³ As modeling higher order interactions between so many brain features (i.e., voxels or regions) becomes complicated for classical statistics, machine learning algorithms are employed.^14,15 These methods, while tremendously promising, must carefully navigate between being over-constraining or too liberal in fitting the observed data if they are to be successful. Tuning mechanisms like regularization control this balancing act by adjusting model bias and variance to achieve better generalization to new, unseen data.¹⁶ That is, hyperparameters for these mechanisms are adjusted before the model is trained, and evaluation on independent data is used to guide selection. This flexible approach allows the error in predicting impairments on new lesions to determine the appropriate level of model complexity for analyzing lesion data.

There are other advantages to using machine learning models for lesion mapping. Better predictions can be achieved because these algorithms can leverage both positive and negative predictors to recognize injuries that elicit an impairment as well as injuries that indicate eloquent cortex is spared. In theory, this ability to pool information across noisy brain regions should allow MLSM methods to achieve more accurate prediction of impairment than LSM.^13,17 However, realizing this potential is difficult.

2. Sources of model inconsistency in multivariate lesion symptom mapping

Most neuroimaging data is affected by spatial autocorrelation.^18–20and lesion mapping is no exception.^11,21–25 In stroke, deficits result from injury along large vascular territories, leading to archetypal injury between individuals and strong associations of neighboring voxels within individuals. These multicollinearities can make it more difficult for models to estimate the independent effects of each predictor on the response variable. Machine learning algorithms can be more robust to multicollinearities for the purpose of making more accurate predictions.²⁶ For example, in the face of redundant features, successful regularization will favor simpler models that are less likely to overfit.²⁶ This minimizes model error by excluding complex relationships, some of which may be genuinely present, thereby undermining the purpose of MLSM.

Much of neuroimaging data also contains irrelevant features, which can introduce noise into the model.²⁷ In the case of MLSM, the goal is typically to relate lesions to deficits carefully isolated by a task to represent some cognitive process. Thus, even ignoring typical sources of model noise in lesion mapping (e.g., inconsistencies in hand drawn lesion masks, poor registration quality, imaging artifacts, measurement noise, etc), we might expect many features to meaningfully predict cognitive processes, but not necessarily those under study. If this form of “noise” is pervasive enough, a model might learn spurious relationships. Thus, the limited learning capacity of a model (e.g., compute available for tuning) might be wasted either attempting to learn from noise, or to distinguish between signal and noise, resulting in a model that does not fully exploit all the available signal.^27–29

Even when the complexity of models is successfully tuned to make good predictions from data with redundant and/or noisy features, they can still produce an incomplete or misleading understanding of feature importance. High feature importance may simply reflect a models’ efforts to make sense of noise.²⁶ When multiple features provide common predictive information, many algorithms will favor one feature over another, which would now no longer provide any unique information to the model. Indeed, some approaches such as LASSO regression explicitly select one of many correlated features for modeling.³⁰ Other approaches like ridge regression adjust the weights of correlated features together, diluting feature importance in potentially counterintuitive ways (e.g., low weights for correlated but highly predictive features).²⁶ Feature dilution over correlated variables affects other algorithms as well (e.g., random forests).^31,32 The most commonly used algorithm in MLSM, support vector machines (SVMs), rely on the same regularization term as ridge regression but uniquely assign feature weights based on their contribution to fitting a regression function within a specified margin of tolerance.³³ This approach can lead to the assignment of high weights to features with relatively low predictive power, a phenomenon that is more pronounced in the presence of correlated features.³⁴ Provided enough feature redundancy or noise in the data, the preference for specific features in machine learning models can shift, reflecting sensitivity to random variations in training data and noise.^28,35 Consequently, the conventional MLSM approach may be able to generate models with good predictive accuracy by ignoring complex patterns of brain damage but may still produce inconsistent feature weights with limited interpretability and generalizability.

In sum, the performance of machine learning is heavily dependent on the hyperparameters that ensure training does not overfit or underfit the data. Critically, for MLSM, there is little guidance regarding how to choose these parameters (though see Zhang et al.,¹⁵; Wiesen et al.,³⁶) as they are typically tuned using the data itself, even though this process can result in poorly generalizable models. There is therefore a need for a principled and robust methods that can help researchers ensure that their models are fully exploiting the signal that is available in the tremendously expensive and often challenging to collect clinical neuroimaging data that they have acquired.

3. Stable multivariate lesion symptom mapping

Here, we propose a flexible pipeline that attempts to improve MLSM models by identifying more reliable features. In conventional MLSM, feature selection is arguably the end goal of the analysis—a model is tuned using all of the features and, after being tested, some method like a permutation test is performed to understand which feature weights are meaningful (e.g., are assigned more importance by the true model than permuted models). We propose an approach we call stable multivariate lesion symptom mapping (sMLSM), where more careful selection of features is the starting point of the model building process. Whereas traditional training selects strong predictors, this approach requires that the selected predictors are reliably strong. Because more reliable or stable features are tuned during model optimization, we expect sMLSM models to potentially generate more consistent feature weights, pick out more complex patterns of damage, and have better generalizability by attempting to limit the models’ exposure to noise or spurious associations.

Implementation of sMLSM requires a single modification to the standard MLSM pipeline: incorporating feature selection within the model tuning process, as illustrated in Figure 1. That is, in conventional MLSM, a machine learning model is trained inside of a nested cross-validation scheme, where non-overlapping partitions of samples are each used to test the model, and the remaining data is used to train it.^37,38 This training data is further partitioned in the same way to generate validation samples that can be used to select optimal hyperparameters for the model, controlling model complexity. In sMLSM, feature selection is performed on the training dataset, prior to tuning, ensuring that the estimate of model generalization remains impartial. Selecting features and tuning a model on the same data can induce overfitting when selecting model hyperparameters.²⁸ To tackle this problem while avoiding nesting a third cross-validation loop (which substantially increases computational time), the training data is subsampled many times in the outer loop.³⁹ Resampling ensures feature evaluation is performed over more datasets that have higher diversity, reducing the influence of noisy data or outliers. Such resampling techniques are often used as an alternative to k-fold for cross-validation.^40,41

In most feature selection methods, out of sample error is used to understand which subsets of features are more generalizable without considering their sensitivity to partitioning noise.^42,43 Our modified approach identifies features consistently selected across perturbed datasets and hyperparameters by some user-selected algorithm, providing an automated and objective method for selecting robust features to model. The generalizability of stable features is subsequently tested by the model for predicting lesion outcome. To this end, we use stability selection, a framework which can be wrapped around any feature selection approach.³⁵ Critically, this method provides some error control, allowing users to identify a stable feature set while attempting to control the upper bound on the number of false positives in this set.

There is no consensus on how MLSM should be performed.^15,37,38,44 and the sMLSM pipeline that we have introduced is flexible enough to inherit many open questions (e.g., which algorithm is best suited to lesion data?). However, in the broader machine learning literature, feature selection plays an important role in improving model performance.^29,45and there is a growing appreciation of this in neuroimaging.^43,46–52

The goal of the present work is to test whether current implementations of MLSM may be discounting the potentially positive impact that feature selection can have on the model and its understanding of feature importance.^53,54 Using a large retrospective dataset of chronic stroke patients with aphasia (N=167) that we have made publicly available,⁵⁵ we implement conventional MLSM, sMLSM, and a simple model that predicts impairment from lesion size alone. We compare how well each of these models predicts lesion outcome in different settings, varying the sample size as well as the number of features submitted to models by using multiple atlases, including a multiresolution atlas. We also test how robust sMLSM is to the primary setting that differentiates this pipeline—the number of false positives that should be controlled to define a stable set of features to model. To better understand the benefits of sMLSM, we assess whether it identifies more complex patterns of damage, evaluate whether it reduces the variance in assigned feature importance, and introduce synthetic lesions to test the pipeline’s sensitivity to multicollinearities as well as the accuracy of error control. Finally, we provide additional external validation of sMLSM by repeating our model training and testing procedure to predict NIH stroke severity scores in an independent acute stroke dataset (N=1106) that has also been made publicly available.⁵⁶ A MATLAB (The MathWorks Inc, 2021) “live-code” notebook is shared to demonstrate these pipelines. This notebook interfaces with an open source toolbox we introduce for stability selection, which implements most feature selection algorithms available in MATLAB’s statistics and machine learning toolbox.

Methods

Participants: chronic stroke dataset

Data collected from one-hundred and sixty-seven individuals with chronic left strokes that participated in studies conducted at the Center for the Study of Aphasia Recovery (C-STAR) was used for all analyses (age at stroke = 57.51 +/- 11.31, 63% male). These data were collected at the University of South Carolina and Medical University of South Carolina. All participants gave informed consent for study participation and the study was approved by the Institutional Review Boards at both institutions. Only neuroimaging and behavioral data from participants’ first visits was utilized where longitudinal data was collected (years post stroke at time of imaging = 3.85, +/- 3.68). All participants had both behavioral and imaging data available for analysis. The median time between collection of neuroimaging and behavioral data was 1 day. This cohort represents a slice of the database that continues to be updated on openneuro and more detailed information about reported as well as additional behavioral and demographic data can be found at: https://openneuro.org/datasets/ds004512/versions/2.0.0.

Behavioral Assessment: chronic stroke dataset

Each participant was administered the Western Aphasia Battery-Revised (WAB-R).⁵⁷ The WAB-R comprises multiple subtests for language impairment in aphasia. The current study utilized the aphasia quotient, which collapses spontaneous speech fluency, auditory comprehension, speech repetition and naming subtest performance into one global score that scales between 0 (reflecting worst aphasia impairment) and 100 (reflecting no aphasia impairment). In the present study, we aimed to predict this severity score.

Imaging data: chronic stroke dataset

Magnetic Resonance Imaging (MRI) was performed at the University of South Carolina or Medical University of South Carolina using a Siemen’s 3T Prisma (Siemens Medical Solutions, 2022) equipped with a 20-channel RF receiver head/neck coil. T1 and T2-weighted structural scans were utilized in the current study. A high-resolution T1-weighted MPRAGE sequence was acquired (matrix = 256 × 256 mm, repetition time = 2.25 s, echo time = 4.11 ms, inversion time = 925 ms, flip angle = 9°, 1 x 1 x 1 mm, 192 slices) with parallel imaging (GRAPPA = 2, 80 reference lines). Three-dimensional (3D) T2-weighted sampling perfection with application-optimized contrasts using different flip-angle evolution (SPACE) was used to acquire T2-weighted sequences (matrix = 256 × 256 mm, repletion time = 3200 ms, echo time = 567 ms, flip angle = variable, 1 x 1 x 1 mm, 176 slices) with parallel imaging (GRAPPA = 2, 80 reference lines).

Image preprocessing: chronic stroke dataset

Lesions were segmented manually using T2-weighted images in MRIcron by a neurologist (L.B.) or a supervised researcher with extensive experience with brain imaging in stroke populations. Both were blinded to behavioral assessments. Lesion masks were resampled to the T1-weighted images using nii_preprocess (https://github.com/rogiedodgie/nii_preprocess/tree/v1.1) and SPM12,⁵⁸ then refined for any necessary corrections in the case that any additional information about lesion extent was revealed by the T1-weighted image. Anatomical deformation during normalization in the presence of large lesions was avoided using enantiomorphic healing⁵⁹ as implemented by the Clinical Toolbox.⁶⁰ In this procedure, the lesion boundary is smoothed and the brain tissue inside the smoothed lesion mask is replaced by intact contralateral tissue, thereby exploiting the natural symmetry of the brain to minimize displacement of voxels relative to other methods when normalizing large unilateral lesions.⁶¹

Regional damage was computed in MNI space for each participant by intersecting their normalized lesion map with several atlases. Our initial analyses focused on the JHU atlas, which represents structural anatomy, including white matter tracts.⁶² Given that more recently available functional atlases may perform better and that it’s unclear what parcellation resolution provides the best-fitting reduction in the dimensionality of the lesion data,^53,63 we also analyzed regional damage within the context of a multiresolution atlas.⁶⁴ Like other functional atlases, this one is defined by clustering voxels into larger parcels with similar activation patterns. However, this atlas is provided with multiple parcellations, where the number of regions increases from 100 to 1000 in increments of 100, reflecting how the clustering solution changes as more clusters are sought. We analyzed all 10 of these parcellations and elected to use a variant of the atlas that includes some anatomical subcortical regions for better lesion coverage.⁶⁵ Despite this effort, smaller coverage resulted in a marginally diminished sample size (N=164).

Participants: acute stroke dataset

Data was used from one-thousand one hundred and six individuals with acute strokes seen at Prisma Health-Upstate in South Carolina from the start of 2019 through the end of 2020. This represents all identified acute stroke encounters over the two-year period after applying exclusion criteria. Participants were excluded if they had subarachnoid, subdural, or intracerebral hemorrhage; stroke mimics, transient ischemic attacks, or other confounding structural or functional brain disorders (e.g., brain tumor, refractory epilepsy). Participants without structural scans or for whom the NIH stroke scale was not collected or recorded were excluded as well. The study through which this data was made available was conducted in accordance with approval received from the Institutional Review Board at Prisma, Requirement for written informed consent was waived as the study was a retrospective analysis of archival data with negligible risk. This data is public and more detailed information about it can be found at: https://openneuro.org/datasets/ds004889/versions/1.0.0.

Behavioral Assessment acute stroke dataset

Each participant was administered the NIH stroke scale, a commonly utilized tool to measure stroke severity in acute ischemic stroke that consists of 11 items, each representing a different aspect of neurological function. The scores on these items are summed to generate a measure of overall stroke impairment that ranges from 0 (no stroke symptoms) to 42 (severe stroke impairment).

Imaging data

The scans collected in individuals were varied. For each participant, T1-weighted, T2-weighted, Fluid Attenuated Inversion Recovery (FLAIR), and diffusion imaging sequences were selected based on optimal brain coverage and signal-to-noise ratio. Scan settings varied across individuals as typical in clinical settings. The specifics of these sequences were documented in a text-based BIDS-format ‘sidecar’ accompanying each NIfTI format image.

Image preprocessing

MRI images were converted from DICOM to NIFTI (Li et al., 2016) and an in-house extension of SPM12’s ‘spm_deface’ script was used to remove features of the neck and face. Lesion masks were manually delineated on the diffusion weighted (TRACE) images by research staff and supervised by an expert with extensive experience drawing lesion masks in stroke populations (R.N.). The Clinical Toolbox⁶⁰ was used to perform segmentation and normalization in a comparable way to the chronic stroke data. The lower resolution diffusion images were coregistered to the higher resolution FLAIRs. FLAIR images were then registered to a common template in order to warp lesion masks from native to standard space. Regional damage was computed in MNI space in the same way as the chronic stroke data.

Analysis overview

Three different models were trained and tested in a repeated, nested, cross-validation scheme: a multivariate lesion symptom mapping (MLSM) model that was exposed to all brain features (i.e., regions of brain damage), a stable multivariate lesion symptom mapping (sMLSM) model that was only exposed to features reliably selected across many subsamples of the training data, and a final lesion model that was only exposed to lesion size as a predictor and with no access to information about regional brain damage. For all models, Support Vector Regression (SVR) was used for prediction as it is commonly employed in MLSM.^37,66,67 Moreover, SVR has remained the predominant machine learning algorithm in stroke neuroimaging, as evidence by trends in PubMed.⁶⁸ Our core analyses evaluated these models relative to each other in chronic stroke, based on out of sample predictions of language impairment. The robustness of our main findings was confirmed by repeating the same procedure in an acute stroke dataset to predict NIH stroke severity scores.

Model cross validation

Cross-validation was repeated 11 times to capture the influence of data partitioning noise, which can have substantial impact on performance estimates.⁶⁹ More repeats are advantageous for narrowing the variability of model performance. We aimed to perform 20 repeats but found this number intractable for the full set of analyses we intended to run to comprehensively characterize the performance of our proposed pipeline. For example, by far the least computationally expensive analysis we performed is presented in Figure 1, where panels A and B alone represent the results of 3,080 models (see caption). Consequently, we stopped all analyses after 11 repeats of cross-validation but emphasize that our point estimates of model performance show clear dissociation. The partitions that we used for training and testing models were preallocated to facilitate more equitable comparisons (i.e., the same test and training samples were used for all models). To ensure data used to test models represented patients with diverse lesion sizes, training and test partitions were stratified by converting lesion size into four distinct categories based on quartiles (0-25^th, 26^th-50^th, 50^th-75^th percentile, 75^th-100^th percentiles). These categories were approximately equal in size (N = 42,42,41,42). Model training and testing was performed over 10 outer folds. Each training dataset from these outer folds was further partitioned using a 4-fold inner loop that was used for tuning models (see Figure 1 for overview).

Figure 1.Schematic showing analysis overview and the difference between multivariate lesion symptom mapping (MLSM) and stable multivariate lesion symptom mapping (sMLSM).

Conventional MLSM involves cross validating a machine learning model in a nested fashion. Inner folds of the cross-validation scheme can be used to tune the model and outer folds can be used to measure the models’ performance. We perform support vector regression tuning with Bayesian optimization for both MLSM and sMLSM models. The sMLSM models differ because they are tuned, trained and tested on features deemed reliable by stability selection. Across 500 subsamples of the training data in the outer fold, the features most consistently selected by an independent algorithm are identified. This process ensures that test data is not used for feature selection and mitigates any overfitting that may occur during validation. The remainder of the pipeline is identical to MLSM.

In sMLSM, stability selection was applied to each training dataset in the outer loop to identify reliable features that were then used for model tuning, training, and testing (Figure 1). Otherwise, tuning and testing proceeded similarly across all models. In all cases, an SVR model was tuned using Bayesian optimization, an efficient search method that learns a function for predicting the performance of different hyperparameter combinations.⁷⁰ Efficient search methods are advantageous for high-dimensional datasets because each evaluation of the model during tuning becomes more computationally expensive, limiting the total number of evaluations that can be reasonably executed and potentially contributing to worse model performance. Bayesian optimization was deliberately chosen to benefit MLSM, which operates over all features in the dataset. We used 50 objective evaluations, wherein the optimizer iteratively updated its understanding of the hyperparameter space. Each evaluation informed the subsequent choice of hyperparameters, striking a balance between exploring new possibilities and exploiting known high-performing regions of this space.

SVR aims to find the best fitting hyperplane for the response variable using the L2-norm of the coefficient vector. To accomplish this, a maximum acceptable error term, ϵ, is tuned for accuracy. As some errors may fall outside ϵ, slack variables are introduced to capture deviations from the margin. An additional hyperparameter, C, tunes the tolerance of the model to such deviations. Here, we tuned ϵ values in the range of [0.39,3.9e+3] and C values in the range [1e-3 1000]. The range for epsilon is determined by an automatically implemented heuristic in the statistics and machine learning toolbox that is based on the interquartile range of the response variable. We also tuned the SVR kernel (linear, radial basis function, or 2^nd order polynomial). In SVR, the kernel trick is used to efficiently transform data into a higher dimensional space through which a hyperplane can be more successfully optimized using different kernel functions. More complex kernels introduce a third hyperparameter, 𝛾, for defining the kernel radius.^33,71 The 𝛾 parameter was tuned using a faster probabilistic method, measuring deviation across subsampled training datasets on a quality criterion.⁷² Note, Bayesian optimization can fail when optimizing more parameters.⁷⁰

Influence of lesion size

Our analyses accounted for lesion size in two ways. First, lesion size was added as a predictor to all models. Second, a model using lesion size to predict aphasia severity was used as a control. Models that better capitalize on information about the location of lesions will better out-perform the lesion size model when predicting out-of-sample data.

Stability selection

The process of stability selection³⁵ distinguishes sMLSM from MLSM. In stability selection, a chosen algorithm is used to perform feature selection on many perturbed datasets using every hyperparameter within a prespecified range, providing a principled framework for injecting noise into the data to evaluate the reliability with which any user-defined feature selection procedure or model makes its selections. As hyperparameters influence feature selection, the stability of a feature is evaluated in the most favorable way possible—according to the most stable settings. That is, for each feature, stability scores are computed by taking the maximum proportion of perturbed datasets in which a feature was selected across all hyperparameter settings. A stability threshold is then applied to these scores to determine a stable set of features. Knowing the average number of features selected across perturbed datasets relative to the total number of features available allows for calibration of the stability threshold based on the empirical probability of selecting features and the expected number of false discoveries. Defining a preferred error rate to control permits selection of a correspondingly stringent enough threshold for defining the stable set.³⁵ Thus, for example, if the feature selection algorithm always selects a large proportion of the feature space, stability must be higher in order for a feature to enter the stable set (see supplemental material for more information).

In line with prior studies, we perturbed training datasets by randomly selecting half of the samples.³⁵ This was repeated 500 times. Feature selection was performed on each subsample using a linear elastic net.³⁰ Although LASSO is commonly used in this context.^35,73 elastic net combines the penalty terms for LASSO and ridge to help address collinearity.³⁰ This helps to ensure that reliably predictive features are selected, even if they share some variance. Elastic net was performed over 1000 log-distributed λ values between 0 and the highest possible value that would return a non-null model, as well as 20 $a$ values where the first value was 0.001 (i.e., ridge regression) and the others were linearly distributed between 0.1 and 1 (i.e., LASSO).

For each subsample, the elastic net was used to select at most just under half of the features in the dataset (e.g., 30 for JHU-MNI). That is, only the first 40% of features that entered the model were retained. This criterion helped enforce regularization during feature selection because the same subset of combined $a$ and λ values could result in no regularization in one perturbed dataset and some regularization in another. We emphasize that stability selection works by capitalizing on variability in feature selection and as the proportion of total features that are selected grows this variability decreases because there are fewer features that could be left out of the selection process.

Tuning the per-family error rate

In the sMLSM pipeline, stability selection acts as a preprocessing step to improve final model predictions and feature weight assignments. Therefore, the goal is to select the largest set of reasonably stable features. One of our interests was understanding how choosing a per-family error rate in stability selection might impact sMLSM prediction accuracy. For instance, it may be the case that only a very small per-family error rate produces models superior to MLSM. Thus, we systematically generated stable sets for each preselected number of false positives in the range [1,28], where 28 was the largest value that produced a stable set not entirely comprised of potential false positives. Each of these stable sets was used to tune, train, and test a different sMLSM model. As an alternative, we tested whether treating the number of false positives as another hyperparameter for tuning could produce equally robust models without requiring manual intervention. Because we had tuned models for 1 through 28 false positives, we simply selected the tuned model with the lowest validation error. However, we made one adjustment—to gently discourage selection of a high number of false positives, which we suspected would be deleterious to models, we applied a linear scaling function,

$$f\left( i,e_{i} \right) = e_{i} \times (1 + k \times i)$$

where $i$ is the number of false positives, $e_{i}$ is the model loss on validation data, and $k$ is a constant scaling factor set to 0.002. This scaling factor was applied consistently across all analyses. The constant value was selected to minimize standard deviation in chosen number of false positives across training folds of the first of 11 repeats of cross-validation. This selection was blind to model performance. However, we also show this value generalizes well in an independent dataset, and in supplemental analyses we demonstrate that performance would have been remarkably similar if a different value was chosen or even no value at all (i.e., no scaling; see supplemental material).

Model performance evaluation

Models were primarily evaluated based on prediction error. We also measured the correlation between predictions and true values. Although it is a highly popular goodness-of-fit measure in predictive models treating neuroimaging data, correlation can poorly reflect a model’s predictive performance because it is translation and scale invariant, sensitive to outliers, insensitive to nonlinearities and biased in some cross-validation schemes.⁷⁴ Consequently, we primarily evaluated model performance using the accuracy percent measure, which expresses in percentage units the mean absolute error of predictions scaled to the error of a naïve model that guesses based on the mean of the training data.⁷⁵

Evaluating feature importance assignment

Differences in model prediction accuracy should be grounded in differences in feature importance. Because we tuned the kernel for SVM, some of our training datasets were fitted with linear kernels such that feature weights directly correspond to a features’ importance. However, other datasets were fitted with nonlinear kernels where feature weights represent the importance of a given feature in the higher dimensional space mapped by the kernel trick. To generate measures of feature importance that could be compared across models with different kernels, we used the algorithm-agnostic Shapley Additive Explanations (SHAP) framework. Shapley values are a game theoretic approach for quantifying the average marginal contribution of a player in a cooperative game.⁷⁶ That is, the Shapley value for a feature describes its role in deviating the prediction from the average or baseline prediction with respect to a specific sample in the data. SHAP is an extension of Shapley values that uses the conditional kernel with k nearest neighbors (corresponding to 10% of the samples) for evaluating feature importance.⁷⁷ Critically, this formulation of SHAP does not assume feature independence. SHAP values were generated for all samples in all training datasets. Because we were purely interested in feature importance and not necessarily the direction in which a feature influenced the prediction, we took the median absolute SHAP values across all 10 training datasets, then samples. How consistently a feature was deemed important across repeats of the cross-validation scheme was then determined by a one tail t-test against zero.

Finally, we compared feature importance for MLSM and sMLSM to univariate lesion symptom mapping (LSM). In this case, cross-validation was not used. Instead, lesion size was regressed out of aphasia severity and one tail independent t-tests were performed between the residuals of patients with lesions and without lesions at different locations in the brain. A brain region was considered lesioned if more than 10% of its voxels were damaged. Regions in which either of the two groups of patients had fewer than 10 samples were excluded from analysis. The analysis was repeated with ten thousand permutations of the residuals to establish significance for each t-statistic.

Results

1. Comparing MLSM to sMLSM across settings for stable feature definition

The sMLSM pipeline introduces a parameter that controls the size of the set of features identified as stable for further modeling. In general, this set can be bigger provided we are comfortable with accepting more potential false discoveries. In comparing sMLSM to MLSM performance, we varied the number of false positives in the stable set used for sMLSM in increments of 1, starting with 1 false positive and continuing up to the point that the number of false positives was equal to the stable set size (Figure 2A). We observed a sharp increase in stable set size as the number of false positives initially increased between 1 and approximately 5. The set size then plateaued as the number of false positives increased. If the goal is to identify the largest set of stable lesion features with proportionally the fewest false positives, this trend suggests that the per family error rate (PFER) should not be set to the lowest setting possible (i.e., the minimum number of false positives that retrieves a stable set) but should remain relatively low.

Figure 2.Stable multivariate lesion symptom mapping improves prediction of impairment.

Stability selection was used to generate stability scores for each cortical and white matter feature of the JHU atlas (left box in panel A) independently in every training dataset (11 repeats of nested 10-fold cross-validation, or 110 datasets). Every set of stability scores was then used to generate 28 different stable sets of features by varying the upper bound on the number of false positives in the stable feature set (middle box in panel A). As the number of false positives increased, the stable set size rapidly increased as well, but quickly plateaued (right box in panel A). At 28 false positives, it was possible for the entire stable set to be false positives. In spite of this, training SVM models on any stable set (3,080 models total) produced predictions that were significantly better than using all features as per standard multivariate lesion symptom mapping (panel B). Mean model performance across all training datasets is presented as dots with standard error of the mean. Mean performance for control models is marked by horizontal dashed lines with shaded areas corresponding to standard error of the mean. The stable false discovery ratio (sFDR) is the proportion of the stable set that may be a false discovery. Models trained only on lesion size performed better than using all features, but worse than any stable set on performance measures based on absolute prediction error (accuracy percent as well as pure absolute error). Adding the number of false positives to the tuning procedure retrieved the highest performing models. Models trained by taking the top n features where n was increased iteratively from 1 to 70 showed a similar overall pattern (panel C). Only when models retained fewer than roughly 45% of the feature set did they begin to perform worse than the lesion size only model.

However, we found that adjusting the PFER had little effect on the discrepancy between sMLSM and MLSM model performance, demonstrating that even stable sets with a relatively large number of false discoveries were preferable to using all features in the data (Figure 2B). Mann-Whitney U-tests between skewed absolute errors made by each of the sMLSM models (per-family error rate; PFER: 1-28) and the MLSM model were all significantly different after concatenation across repeats of cross-validation (CV; maximum FDR-corrected p-value was p < 0.01), with sMLSM models producing lower errors (see live code notebook section, “Formally testing for differences between sMLSM, MLSM and lesion size models” for more testing information and pre-generated figures). The same trend was observed for comparisons between sMLSM models and the lesion size only (LSO) model (maximum FDR-corrected p-value was p < 0.05). The LSO model performed surprisingly well when averaging accuracy percent and correlation across repeats (i.e., based on standard error of the mean or SEM across CV repeats; Figure 2B). However, it did not show significantly lower absolute errors than the MLSM model when concatenating all predictions together, Z = 0.91, p = 0.36. Thus, while LSO may perform more consistently across different data subsets (i.e., partitions) because it contains only a single feature, this consistency does not imply uniformly better performance across all individual instances of the dataset when compared to MLSM. To confirm this effect was not driven by the dependence between samples partitioned together, we also performed a corrected repeated k-fold CV t-test between model errors,⁷⁸ t(109) = 1.33, p = 0.09.

Within the batch of sMLSM models tested, we did observe a general trend wherein a higher stable false discovery ratio (sFDR, or the PFER divided by the stable set size) was associated with worse performance and the best models had relatively low PFER. We tend to focus on sFDR where possible as it is more intuitive, reflecting the proportion of discoveries that may be false, and assigns lower rank to low PFER values that result in such small stable sizes that the proportion of false discoveries is relatively high (e.g., see 1 false positive sMLSM models in Figure 2B). Accuracy percent was inversely correlated with sFDR, r(26) = -0.63, p < 0.001 as was the correlation between predicted and true values, r(26) = -0.66, p < 0.001. Across repeats of CV, correlation performance for sMLSM was more similar to LSO at higher sFDR. Note, however, prediction error was still lower (i.e., accuracy percent).

2. Tuning the stable set in sMLSM models

While sMLSM was robust to PFER choice for improving on MLSM and LSO models, performance was more consistent at lower PFER. Automatically tuning PFER produced good models without user intervention, suggesting this to be a viable approach for establishing this parameter (Figure 1B). Tuning did not purely favor the lowest PFER values. The median PFER that was selected was 2.8 and corresponded to a median sFDR of 0.12 in a median stable set size of 21. That is, generally, 28% of features were retained in sMLSM and 12% of those features may have spuriously appeared to be stable. Absolute prediction errors were significantly lower for the tuned sMLSM model than the LSO model, Z = 4.5, p < 0.00001 and for the tuned sMLSM model than the MLSM model, Z = 5.1, p < 0.00001.

In another strategy for defining the stable set in sMLSM, we retained the top n stable features, and varied n from 1 to 70 (Figure 2C). Retaining less than 55% of features was necessary for more distinctly outperforming MLSM and roughly 40% of features for outperforming LSO models. This may be another viable strategy for defining stable sets without intervention. However, successfully tuning n for a particular dataset may be more difficult since the parameter space is wider, and it is less meaningful than PFER or the corresponding sFDR.

The features identified by tuning sMLSM were confirmed to be more meaningful than feature selection by chance according to both accuracy percent and correlation (p < 0.0001). Due to memory constraints, this test was not performed on absolute prediction errors across all repeats of CV. Instead, mean correlation and accuracy percent was computed over repeats. In this analysis, we performed repeated CV 500 times, each time selecting features for modeling at random based on the size of the stable sets in the tuned sMLSM models (see live code with pre-generated figures in the “Testing random feature selection” section). Random selection of features also resulted in models that did not perform differently from MLSM on accuracy percent, p = 0.51 or correlation, p = 0.8.

3. Influence of sMLSM on feature importance

The predictions for MLSM, sMLSM and LSO models are presented as scatter plots in Figure 3A. Here, predictions were collapsed across repeats of CV to form ensembles for each model, resulting in slightly better performance (c.f., Figure 2B and 3A). Performance was notably better for MLSM, indicating higher variance in model performance due to partitioning noise.

Figure 3.Consistency of feature selection in stable multivariate lesion symptom mapping.

Model ensembles are formed by averaging aphasia severity predictions across all stable multivariate lesion symptom mapping models (sMLSM), conventional multivariate lesion symptom mapping (MLSM) models (i.e., models trained on all features), and models trained only on lesion size. Ensemble predictions for each sample (represented by dots) are presented in panel A. The sMLSM models show a bimodal distribution of feature selection across repeats of cross validation, indicating that features were either consistently excluded or consistently selected across repeats (distribution in panel B). The standard deviation of feature weights (as averaged across training datasets within each repeat) are lower across repeats of cross validation with sMLSM than MLSM (panel C). Standard deviation of features in MLSM models was subtracted from standard deviation of features from sMLSM models (x-axis in panel C). Difference in deviation was unrelated to variance inflation factor for features (y-axis in panel C).

The proportion of repeats of CV in which a feature was selected during sMLSM was bimodal, reflecting overall good consistency of stability selection in sMLSM across repeats (Figure 3B). However, a minority of features were selected in some repeats but not others, indicating stability selection is not immune to overfitting to partitioning noise. This aligns with the median sFDR of models and datasets with more power may be able to produce non-empty stable sets for lower PFER.

Standard deviation in feature importance across repeats of CV was evaluated to understand whether sMLSM helped to stabilize weights. The skewed standard deviation of SHAP values, reflecting gross feature importance to model predictions, were lower for sMLSM than MLSM, Z = 3.2, p < 0.01. When focusing only on features consistently selected by stability selection (i.e., selected in at least 80% repeats of CV; Figure 3C), the effect was stronger, Z = 3.7, p < 0.001. Only a single consistently selected feature showed markedly more deviation in sMLSM than MLSM. The difference in SHAP deviation between the two models was not related to feature Variance Inflation Factors (VIFs), showing stabilization across levels of multicollinearity, r(75) = 0.02, p = 0.98.

Feature importance was visualized to qualitatively appreciate whether model performance in sMLSM stemmed from identifying different patterns (Figure 3). Models were also compared to LSM, which primarily highlighted posterior insula, postcentral, supramarginal, angular, and parahippocampal gyri. MLSM downweighed the role of inferior parietal regions and generally placed stronger emphasis on anterior regions. These included pars opercularis of the inferior frontal gyrus, the precentral gyrus, anterior insula, and anterior superior temporal cortex. In addition, MLSM placed high importance on the superior temporal gyrus and posterior middle temporal gyrus. sMLSM placed highest importance on the same regions highlighted by LSM except the parahippocampal gyrus, while also emphasizing superior temporal gyrus and posterior superior temporal gyrus (see also Table 1 for effects in white matter regions).

Evidence that sMLSM picked out more complex patterns was also present during the tuning process. In sMLSM, 94% of models were tuned to use the radial basis function (RBF) kernel. In contrast, only 31% of MLSM models were tuned to use the RBF kernel and 68% of models were tuned to use the linear kernel.

Figure 4.Feature importance varies across models.

Mass univariate lesion-symptom mapping (LSM) with a permuted t-test is shown in panel A. Brighter yellow colors represent higher test statistics. Feature importance for multivariate lesion symptom mapping (MLSM) is shown in panel B and feature importance for stable multivariate lesion mapping results (sMLSM) is shown in panel C. The sMLSM and MLSM t-statistics reflect a one-tail t-test against zero for absolute SHAP values across repeats of cross-validation (i.e., gross feature importance capturing linear and nonlinear effects as well as interactions).

4. Influence of sample size on models

To establish the influence of sample size on sMLSM (tuned for PFER), MLSM, and LSO models, we drew random subsamples of the data based on 6 sample sizes ranging from 35 to 155 in increments of 20. For each sample size, 60 random datasets were constructed and submitted to our repeated nested cross validation scheme. Measures of accuracy percent and correlation were averaged across all 60 datasets to produce a point estimate of model performance for a dataset of a certain size. For brevity, trends are summarized based on SEM for model performance across all datasets (i.e., whether there is overlap).

Strikingly, LSO models performed relatively similarly across sample sizes, while sMLSM and MLSM models benefitted much more from access to larger sample sizes (Figure 5). At smaller sample sizes (35-55), sMLSM improved model prediction error over MLSM as reflected in correlation, but did not show better accuracy percent. The linear relationship between model performance and sample size as measured by the variance explained by a linear regression was higher for sMLSM than MLSM, both of which were substantially higher than LSO, suggesting that sMLSM may be able to generate better models in relatively smaller large datasets (Figure 5). It may be that MLSM models begin to plateau at sample sizes of 155-167, though this is not clear from our simulations and more data is needed. Moreover, sMLSM models showed a pronounced improvement in performance at these sample sizes.

Figure 5.Effect of sample size on multivariate lesion symptom mapping.

For each specified sample size (i.e., N=35, 55, 75, 95, 115, 135, and 155), a total of 60 subsamples were taken from the entire dataset (N=167). The cross validated performance of multivariate lesion symptom mapping (MLSM; purple), stable multivariate lesion symptom mapping (sMLSM; yellow), and a lesion size only (pink) model was measured across all subsamples. Each dot represents mean model performance (accuracy percent in panel A and correlation coefficient in panel B). Error bars represent standard error of the mean. Graphs on the left show linear regression trend lines extrapolated to larger sample sizes for each type of model. Graphs on the right show actual model performance across subsamples (as well as performance when models were fit to the entire dataset; N=167).

5. Influence of feature dimensionality on models

A functional multiresolution atlas (see methods) was used to evaluate how feature dimensionality impacted models. Performance of MLSM on all 10 resolutions of the Schaefer atlas was measured. For brevity, we summarize comparisons between models based on SEM across repeats of CV. Performance was not correlated with the number of features in the atlas (p > 0.05), but the highest resolution atlas tended to perform better than the others (Figure 6A). This resolution (1000 total features, but 406 that overlapped with lesions) was also the only one to outperform the JHU atlas (Figure 6A) on both correlation and accuracy percent.

Figure 6.Effect of atlas dimensionality on stable multivariate lesion symptom mapping.

Multivariate lesion symptom mapping (MLSM) was performed for a multi-resolution functional atlas⁶⁴ and performance was compared to MLSM of the anatomical JHU atlas (panel A, top scatter plots). As no strong association between model performance and atlas resolution emerged, half of the multi-resolution parcellations were used to perform stable multivariate lesion symptom mapping (sMLSM; panel A, bottom row of brain projections). Note, the number of features in the atlas that contained lesion information are shown in parentheses. The performance of sMLSM models as a function of increasing the upper bound on number of false positives in the stable sets (i.e., from 1 to 30) is shown separately for each atlas (panel B). Tuning the number of false positives in the sMLSM model for every training dataset often resulted in better performance and always outperformed the lesion only models and the MLSM models. The tuned sMLSM models trained on features of the functional atlas often slightly outperformed the tuned sMLSM models trained on the JHU atlas on our main performance measure, accuracy percent (panel C).

Due to computational constraints, we analyzed every other atlas resolution for sMLSM and LSO models. Here, again, PFER rates were systematically varied, revealing similar overall patterns. One point of difference, however, was that some atlas resolutions induced a high degree of variance in model performance based on SEM across cross-validation repeats, likely reflecting poor fit of atlas resolution to the data (Figure 6B). Further, not all atlas resolutions showed a decreasing trend between model performance and sFDR (c.f., Figure 2B and 6B). However, tuning PFER in the models trained on different atlas resolutions consistently gave good solutions, sometimes outperforming the preselection of any single PFER value (Figure 6B). As we observed with the JHU atlas, tuned sMLSM models always outperformed MLSM models by a large margin and outperformed LSO models as well. Just as for MLSM, there was no observed relationship between model performance and atlas resolution in sMLSM (Figure 6C).

6. Testing sensitivity to multicollinearities and accuracy of false discovery estimation under simulated conditions

We explored sMLSM and MLSM behavior under simulated conditions. To understand how the models performed in the presence of a greater degree of multicollinearity, we synthesized 100 multicollinear features and added them to the dataset (i.e., JHU features), corresponding to a ~130% increase in dimensionality. This process was repeated 50 times. Multicollinear features were synthesized from the set of features that significantly correlated with the response variable at p < 0.01 (71% of total features). As this set was relatively large, we first randomly selected a pool of 30% of the significantly correlated features. From this pool, 2 different features were chosen at random to create a multicollinear feature by computing the dot product between the selected features and random coefficients between 0 and 1. A noise term was then added from a normal distribution with a standard deviation scaled by 0.1 to ensure a relatively close relationship to base features while exhibiting some variability. The performance of sMLSM was unimpacted by the increased multicollinearity (c.f., Figure 7A and 2B). Meanwhile, MLSM benefitted from the additional features (c.f., Figure 7A and 2B). While sMLSM still outperformed MLSM in this experiment, the results indicate that substantially greater redundancy of signal helped MLSM focus on modeling predictive patterns and to avoid modeling noise, while sMLSM was already highly effective at capturing the predictive signal available.

Figure 7.Model behavior under simulated conditions.

In panel A, MLSM and sMLSM model performance is shown when the feature space is increased by ~130% by introducing synthetic multicollinear lesion data. Mean model performance is indicated over 50 repeats of adding synthetic features with bars showing standard error of the mean (SEM). While sMLSM performs better than MLSM, there is no shift in performance as a function of introducing these synthetic features (c.f. tuned sMLSM in Figure 2). In contrast, MLSM performs slightly better with substantially increased multicollinearity (c.f. Figure 2). In panel B a varying number of noise features are added to the most highly correlated features with language impairment (top 50% or N = 38) to generate datasets of 100, 200, 300, 400, 500, 600, 700, 800, 900, and 1000 features. This is repeated 5 times and stability selection is performed on each dataset using between 1 and 30 false positives to estimate the stable set. The number of true negatives (proportion of total noise features removed by stability selection), true positives (proportion of signal features retained by stability selection) and false positives (proportion of retained features that are noise) is plotted for each result of stability selection. Dotted lines represent the mean for a dataset. Line colors correspond to the total number of features with brighter colors representing larger datasets. The proportion of false discoveries is shown as a function of the estimated number of false positives used to define the stable set (bottom left chart) and the estimated proportion of false discoveries based on the size of the resulting stable (bottom right chart).

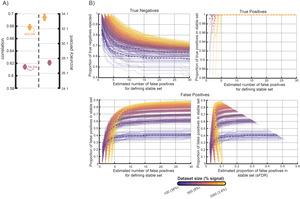
In another analysis, we systematically added increasing amounts of noise features to a core set of features highly correlated with language impairment to assess the accuracy of error control in stability selection during sMLSM. First, we identified 50% of the features most highly correlated with impairment (N=38). We then randomly selected features from this pool, permuted them, and combined them with the highly correlated features. This process was repeated to create new datasets ranging from 100 to 1000 features in increments of 100, corresponding to scenarios where between 38% and 3.8% of features represent signal. The procedure was repeated 5 times. In each resulting dataset, stability selection was performed with identical settings to previous analyses on one repeat of our cross-validation scheme. A range of stable sets were generated by controlling the estimated number of false positives (NFPs) to range between 1 and 30.

We found stability selection robust under these conditions at identifying the majority or all signal features irrespective of the NFP setting (Figure 7B), bringing our empirical results from previous analyses into context. Stability selection was also effective at removing noise features, successfully eliminating between approximately 60 and 100% of the noise, depending on the specific signal to noise ratio and the estimated NFP. In general, the true proportion of the stable set that represented false discoveries was higher in smaller datasets characterized by a larger proportion of signal to noise (i.e., datasets with 100 and 200 features, and 38% and 19% signal). In these smaller datasets, the proportion of the stable set estimated to be a false discovery tended to be lower than the true proportion of false discoveries. In the remaining datasets (300-1000 features with 13% to 3.8% signal), the estimated false discoveries were accurate or more conservative than the actual number of false discoveries, but only when the estimated number of false positives was particularly low (i.e., one of the smallest values that could be set to produce a stable set). Overall, this supports our findings with real-data, underscoring the importance of tuning the NFPs to clarify the degree to which the model used for estimation can cope with some of the noise that can be retained during feature selection. It also confirms an alternative strategy that can be successful—selecting one of the lowest possible values that can retrieve a stable set of features (see Figure 2 for cases where the absolute lowest value may not be appropriate).

7. External validation of model performance

Our core findings are based on out-of-sample model performance in chronic stroke. We tested whether the same patterns would emerge in an independent dataset, using the same repeated, nested, cross-validation scheme in Figure 1 but while reducing the number of repeats from 11 to 10. In this case, models were trained to predict NIH stroke severity scores from lesion maps drawn on clinical scans. First, we performed this analysis on a subset of individuals to more closely match the sample size of the chronic stroke dataset we previously used. We achieved this by excluding all individuals with left hemisphere or cerebellar lesions (N = 275). Using the same parameters for sMLSM (i.e., linear scaling, maximum features retained per subsample, etc), we found an overall similar pattern of performance, with sMLSM performing substantially better than lesion size and lesion size performing better than MLSM (Figure 8). Our sample size simulations in chronic stroke suggest that: i) expanding the sample size to one thousand or more individuals substantially shrinks differences in performance between MLSM and sMLSM, and ii) MLSM outperforms lesion size models. Testing our models on the entire acute stroke dataset (N = 1106) shows that MLSM massively benefits from the larger sample size as anticipated. Further, sMLSM confers a small but significant increase in model performance as measured by a paired t-test for both correlation, t(9) = 2.4, p < 0.05, and accuracy percent, t(9) = 2.4, p < 0.05. Notably, differences were starker when omitting the linear scaling function used to push tuning of stability selection towards lower estimated number of false positives for defining the stable set for both correlation-based performance, t(9) = 5.8, p < 0.001 and accuracy percent, t(9) = 5, p < 0.001. Post-hoc analyses with chronic stroke data suggest introducing linear scaling can have a small positive impact on model performance (see supplemental material). This is because out-of-sample estimates of performance can be less reliable when the test sample is smaller.⁷⁹ However, we emphasize that even in the chronic stroke data, omitting this scaling factor did not produce a meaningful difference in model performance.

Figure 8.Validating sMLSM in external data with larger sample size.

New sMLSM (purple dots), MLSM (yellow dots) and lesion size models (pink dots) were trained to predict NIH stroke severity in an independent dataset of acute stroke patients. Panel A shows mean model performance on a smaller subset of the dataset with right hemisphere lesions that more closely match the size of the chronic stroke dataset from preceding analyses. Bars represent standard error of the mean across repeats of cross-validation. Panel B shows model performance on the entire dataset. Panel B also depicts the performance of sMLSM when the estimated number of false positives is tuned without a linear scaling function (beige).

Discussion

Machine learning models are judged on prediction accuracy, but in neuroimaging, they are also expected to provide insight into neurobiology.⁷⁴ Consequently, most machine learning pipelines separate an initial model development stage with a subsequent interrogation of the model to identify which features are important.⁸⁰ Here, we improved the prediction of aphasia severity from lesion location by identifying features that more reliably predict impairment across many perturbed datasets and hyperparameter configurations during model development. We show that this pipeline, which we call stable multivariate lesion symptom mapping (sMLSM), not only produced more accurate predictions than conventional multivariate symptom mapping (MLSM) or a model that only contained lesion size as a predictor (lesion size only model, or LSO), but also focused on more complex patterns of brain damage and assigned feature importance more consistently over different data partitions. This performance advantage was validated in an independent acute stroke dataset while training models to predict overall stroke severity using a similar sample size as well as a much larger sample size.

On closer inspection of the features that drove model performance, we found that sMLSM was able to capture the significant associations revealed by univariate lesion symptom mapping (LSM) while still implicating some of the many additional regions that were highly influential in MLSM. Overall, sMLSM more clearly captured regions previously associated with aphasia severity in the lesion mapping literature. For example, sMLSM more strongly implicated the superior temporal gyrus⁸¹ and unlike MLSM, it supported the role of inferior parietal cortex, which was also highlighted by LSM in our study as well as prior work.⁶⁶ Our MLSM models strikingly placed higher emphasis relative to the other methods on frontal regions, which have been implicated in prior MLSM work.^38,67,82 These observations suggest that sMLSM can potentially provide more meaningful insight into brain-behavior relationships.

1. Lesion size as a robust predictor of aphasia severity in smaller sample sizes

At first glance, it may seem surprising that lesion size, a relatively crude stroke feature that lacks information about location of brain damage, sufficed as a remarkably accurate and consistent predictor of both aphasia severity in chronic stroke and overall severity in acute stroke. Indeed, when we randomly subsampled our chronic stroke dataset to understand the influence of sample size on our models, we found that the LSO model tended to produce substantially lower prediction error than either sMLSM or MLSM models, up to a sample size of approximately 75, after which only sMLSM began to outperform LSO, particularly as sample sizes approached 155. This finding aligns with recent work in a much larger sample of acute stroke patients (N=753), which has found lesion size to slightly underperform compared to MLSM for predicting stroke severity, and to perform as well as MLSM in sample sizes of 50 and 150.⁴⁹ While our findings in chronic stroke are slightly less optimistic about the value of lesion location in MLSM, we note that our results indicate the pattern of worse performance can be explained by strong sensitivity to partitioning noise. That is, despite producing on-average higher prediction error across repeats of nested cross-validation, MLSM models did not demonstrate significantly higher prediction error when aggregating predictions across all repeats in an ensemble-like fashion. Thus, our results suggest that in larger sample sizes, MLSM can perform as well as LSO provided that the variance introduced by partitions is taken into account. Reassuringly, our sample size simulations in chronic stroke indicate that larger sample sizes provide a substantial boost to sMLSM performance across repeats of cross-validation. Consistent with this, our external validation of models in acute stroke showed similar patterns of performance in a sample size of 275 but saw MLSM outperform LSO and perform marginally though significantly worse than sMLSM in a much larger sample size of 1000. The performance we achieved in the acute stroke dataset aligns with results from other recent work predicting stroke severity in a similar sample size.⁴⁹

A common explanation for the robust performance of lesion size as a predictor of aphasia severity is that larger lesions will tend to impinge on larger portions of the language network, resulting in more severe language impairment (DeMarco & Turkeltaub³⁷ but see Sperber⁸³). From first principles, larger lesions are more likely to include critical nodes for modular functions, as well as include sufficient degradation for distributed processing. However, because patients may exhibit a similar degree of language impairment while having problems with different aspects of language that are localized to different portions of the language network, lesion location may play a greater role in models that seek to predict more specific language deficits than we focused on here.⁶⁶ At the same time, aphasia results from damage to the language network, suggesting that lesion location should provide some information about the deficit. Our work confirms this general claim, but only when models are exposed to a large enough sample size and a smaller set of reliable features is identified for modeling. Indeed, we highlight the exciting prospect that lesion mapping studies are only now achieving the kinds of sample sizes that are necessary to start successfully leveraging information about lesion location. In contrast, we found that lesion size tends to perform similarly across different sample sizes, implying that it may be a better stroke biomarker in smaller studies.

2. Improving models trained on neuroimaging data through identification of stable features

The sMLSM method improved prediction of impairment by selecting reliable features for model training. Random selection of features matched for size performed significantly worse than sMLSM as well as MLSM, indicating that selected features better predicted impairment than chance, and that MLSM was able to exploit limited information about lesion location. Further, we found sMLSM to be less sensitive to redundancies in the data, showing similar performance when a large degree of multicollinear synthetic lesion data is introduced. Notably, feature selection algorithms are not guaranteed to improve models. The effectiveness of traditional feature selection algorithms significantly diminishes in relatively smaller sample sizes. This is due to their tendency to overfit, which results in selecting features that perform well on specific small datasets but poorly on others. In such cases, the chance of these algorithms consistently identifying the truly relevant features is markedly low.⁸⁴ Stability-based feature selection offers a compelling solution to this problem. These methods prioritize the repeatability of feature selection across different subsets of the data and various modeling techniques, identifying features that consistently contribute to the model’s predictive power across different data splits and modeling scenarios. The repeated affirmation of a feature’s importance reduces the impact of random noise and peculiarities present in small datasets, leading to a more reliable and generalizable selection of features.⁸⁵ This ensemble approach to feature selection shares conceptual similarity with the influential bootstrap aggregating method for improving model prediction accuracy by averaging out the biases of many individual models.^86–88 Further, by focusing exclusively on prediction error, most feature selection approaches fail to consider that their solutions may be difficult to interpret because different subsets of features can result in similar prediction error. In contrast, feature stability is an indicator of biomarker reproducibility,⁸⁵ and stability-based feature selection methods have been highly successful in microarray analysis and chemometrics,^89–92 as well as other applications ⁹³. Here, we contribute to this body of work in the context of lesion mapping, showing that the identification of stable features can improve models trained on this kind of data provided they have access to adequate sample sizes.

A small group of neuroimaging studies have previously leveraged stability analysis with success outside of lesion mapping and our approach may be relevant to other modalities.^{46,48,73,94–97} While many of these prior studies diverge from our approach, either because they operationalize stability analysis outside of the stability selection framework or use stability selection outside of a regression or classification model building procedure (e.g., for discovering features), some share many similarities. For example, Rondina and colleagues⁴⁸ found that in a functional MRI dataset that contained roughly 916 features for each sample, stability selection was too stringent and proposed a substantially modified procedure. Here, we demonstrated that after atlas-based dimensionality reduction, stability selection was able to retrieve stable feature sets that improved model performance. Moreover, we tested whether varying the per-family error rate, which controls the stable set size, had a substantial impact on model performance, finding that while a successful approach was to tune this parameter using out-of-sample error, any selection where fewer than all of the features were possibly false positives tended to result in improved prediction accuracy by removing some noise.

In many cases, the most accurate models we trained maintained a low but not the lowest per family error rate possible. This aligns with observations that there can be a tradeoff between stability and accuracy in models, and that models may perform best when these measures are considered together.^94,96,98 It is also consistent with our experiments in adding varying degrees of synthetic lesions uncorrelated with impairments to our data. Although stability selection could retrieve the majority or all strongly correlated lesion features at the lowest per-family error rates, it tended to quickly accumulate false positives in a way that outstripped its estimate of false discoveries, despite still providing a way to eliminate most noise features. Thus, tuning this error rate parameter using out-of-sample error can be particularly effective as it evaluates how well the model used for estimation in sMLSM can handle varying degrees of false positives while balancing efforts to retain as much reliable signal as possible. In smaller datasets than we have focused on, it may be helpful to bias sMLSM tuning towards smaller per family error rates as such datasets are more likely to produce unreliable estimates of model error.^79,99,100 potentially swaying selection towards feature sets more likely to cause overfitting. We attempted such an approach but found it only had an insignificant positive influence in the chronic stroke dataset and a deleterious influence on the much larger acute stroke dataset.

In a study that bears some similarity to ours, Jollans and colleagues⁴⁶ predicted functional outcomes in a large cohort of individuals wat high-risk of psychosis and recent-onset depression using a combination of real and simulated functional and structural MRI data. These authors report that using an external feature selection step that involved stability analysis as well as evaluation of out-of-sample error improved model performance in some cases, but particularly when sample sizes were relatively smaller and there were many features. Our findings are compatible even though their study only considered linear effects during modeling and feature selection was not multivariate. We found the sMLSM pipeline to bring most benefit to datasets with moderate sample sizes (N > 75). However, we also show that it may continue to offer some smaller improvement in much larger datasets (i.e., N = ~1000). This is because stability selection helps exclude features that may influence the model only as an artifact of sampling variability, which happens to be higher in smaller datasets. It is worth pointing out then, that stability selection can have a greater impact in larger datasets if the number of features increases. Thus, we expect sMLSM to benefit regional lesion mapping in typical sample sizes and voxelwise lesion mapping in the kinds of large-scale stroke datasets that are only now becoming available.

In the context of the type of data analyzed here, sMLSM may more effectively detect subtle clinically relevant patient features and characteristics that improve prediction of patient outcomes, and which might not be as apparent in smaller datasets. Furthermore, even the smaller improvements that sMLSM can afford may become more significant as large datasets become more granular, increasing the richness and number of collected measures.

3. Considering data dimensionality for sMLSM

Some prior work has studied whether MLSM is sensitive to different strategies of feature selection, including functional and structural atlases as well as data-driven dimensionality reduction performed over voxels.⁵³ Although we described a very different method for feature selection grounded in stability analysis that improved MLSM performance, our results broadly support that choice of atlas has at most a small impact on model accuracy.⁵³ In MLSM, we found that functional and structural atlases with relatively few features (<76 represented features) produced results comparable to functional atlases with many more features (>250 represented features). While we observed markedly better performance with MLSM when using a very high-resolution functional atlas (>400 represented features), a similar improvement was not found for sMLSM, where most functional atlas sizes resulted in comparable performance. The meaning of this is unclear as there is no overall relationship between atlas size and performance, and it may simply be the case that this particular functional atlas happened to be a better fit to our data. In contrast, sMLSM tended to perform slightly better with functional atlases, however, we cannot exclude the possibility that performance simply plateaued when a functional or structural atlas contained at least 176 features. Ultimately, it is possible that functional atlases may better represent localized impairments by less closely following the topographic bias of lesions towards vascular territories^53,83 and more work is required to understand how atlases generated from groups can be better fit to individuals to potentially improve model accuracy.¹⁰¹

4. A toolbox for stability selection and code for sMLSM

One of the exciting aspects of the stability selection approach that we have employed in this study is that it is highly flexible, and its settings can be automatically tuned to produce well-performing models while lowering the burden on users. As an ensemble feature selection method, it may be used to fuse multiple complementary feature selection approaches to identify more unique subsets of features than we were able to investigate here. While recent packages have been implemented for stability selection in R¹⁰² and python (https://github.com/scikit-learn-contrib/stability-selection), much of the neuroimaging community relies on MATLAB for preprocessing and analysis.¹⁰³ We have publicly published a MATLAB toolbox for stability selection that implements 20 different classification and regression algorithms in MATLAB’s statistics and machine learning toolbox. We acknowledge that MATLAB itself is not open source. However, given its popularity in the neuroimaging community, we hope our implementation can facilitate the adoption of what we believe to be a powerful analysis tool that can benefit many researchers in the community.

We additionally see this package as an opportunity to highlight to researchers the dangers of data leakage that have become problematically common in neuroimaging studies,^74,104–113 and package our toolbox with a variety of tutorials for implementing appropriate cross-validation with feature selection. This includes a live code notebook containing code for replicating the MLSM and sMLSM pipelines that we have presented here.

5. Limitations and future directions

The sMLSM pipeline that we have introduced has not been tested on a wide range of datasets. Therefore, it is uncertain whether it would perform as well in the context of other behavioral impairments or imaging modalities, particularly as the impairment measures we focus on here are quite broad, capturing many different types of impairments, even when constrained to the domain of language function. While we have taken care to select reasonable settings for stability selection and have explored the impact of some settings on model performance (e.g., per family error rate), much work is needed to address how other settings may influence the results (e.g., feature selection algorithm, prediction algorithm, number of data perturbations, resampling technique, proportion of data selected in each sample, hyperparameter ranges for consistently adequate feature selection, etc). For example, a range of cutting-edge feature selection methods have been successfully used in a broader neuroimaging context than we have focused on here and may be implemented within the stability selection framework.^114,115

Future work aimed at understanding these aspects of the sMLSM pipeline will benefit from testing even more well-defined problems with artificial lesion data than we were able to here. While stability selection, underpinning our sMLSM pipeline, has been applied to a variety of toy and real datasets, its behavior in the context of the specific problems encountered in lesion symptom mapping is unclear (e.g., bias towards vascular trunks) and warrants further, careful, attention. Indeed, our finding that stability selection can be too conservative at low per family error rates and too liberal at higher rates suggests that this approach may be better suited to analyses where the stable set can be refined if false positives are encountered. Work on stability selection and error control is ongoing.^88,116–119

Future studies focused on developing predictive multivariate lesion symptom mapping models should also make use of recently available large-scale stroke datasets like the ones we have showcased here. While simulations provide a controlled environment for better understanding the behavior of a pipeline, the ultimate purpose of the pipeline is to achieve better prediction accuracy on real-world data, representing a more useful understanding of the neural correlates of the behavioral impairment under study. We emphasize that these approaches are complementary. For example, while here we have shown that sMLSM outperforms the conventional pipeline in the field, it is entirely possible that it is less sensitive to certain patterns in the data that have low but real predictive value. Simulated scenarios can more clearly highlight such possibilities and help to improve modeling efforts.

We also note that the additional computational requirements imposed by stability selection make permutation testing for feature importance after model building more difficult. In our study, tuning the per family error rate for sMLSM was inefficient as we first tuned each stable set formed across a range of error rates to investigate sMLSM behavior. Future studies can directly tune this parameter, particularly using an efficient search strategy such as Bayesian optimization, to greatly improve the feasibility of permutation testing.

While sMLSM and feature selection can benefit models trained on relatively smaller sample sizes, it is worth noting that it may have little impact on larger industry-sized datasets, where the edge case outliers and idiosyncrasies are ignored due to consistent signal of strong predictors. The sample sizes at which sMLSM will no longer be beneficial are unclear and inexorably linked to a number of different factors, including the number of features available to model, the complexity of the model, the task at hand, and the amount of signal versus noise in the predictors and response variable.

In the current work, we have tried to ensure that our models are trained and evaluated on datasets with representative lesion distributions (i.e., cross-validation stratified by lesion size). We are not aware of MLSM studies that have previously taken this step, but believe it is important for future work to consider the problem of randomly drawing representative datasets for cross-validating models more carefully, especially when performing k-fold cross-validation with high k, which defines a larger number of smaller datasets. Given the small but unique contribution of lesion location to model performance in the current work, it is also important to consider covariate shift for all predictors. Regression problems dominate lesion symptom mapping and are not commonly associated with stratification by the response variable, however, this technique may also help ensure more representative partitioning of the data. Finally, future investigations may benefit from predicting impairments in smaller lesions, which tend to be both more difficult to model but also more helpful for understanding the extent to which lesion location can offer predictive information beyond lesion size.

Code and data availability

Our MATLAB stability selection toolbox is available at: https://github.com/alexteghipco/StabilitySelection. The live code notebook showing implementation of MLSM and sMLSM pipelines can be found here: https://github.com/alexteghipco/StabilitySelection/blob/main/Tutorial3_PredictLSM.mlx. See notebook for links to dependencies and preprocessed data used for analyses, otherwise the same chronic and acute stroke data can be downloaded in BIDS format on openneuro using the following links https://openneuro.org/datasets/ds004512/versions/2.0.0 and https://openneuro.org/datasets/ds004889/versions/1.0.0

Acknowledgements

This work was supported by grants from the National Institute of Health and National Institute on Deafness and Other Communication Disorders (P50 DC014664, U0 1DC011739, R01 DC008355).

Competing Interests

The authors report no competing interests.