Introduction
Neuroimaging has emerged as a powerful tool for studying brain function and connectivity, offering insights into the underlying neural mechanisms of various cognitive processes and disorders. Preprocessing and analysis of neuroimaging data require sophisticated tools to extract meaningful information. FSL1 is a widely used2 software package in the field of neuroimaging, offering a comprehensive suite of tools for neuroimaging data analysis. Indeed, a Google Scholar search lists 3030 publications for the term fsl software package in 2022. The command line tool fslmaths is central to FSL, enabling advanced image manipulation and processing: it can be used as a standalone application for basic manipulation, but is also leveraged by many of the other FSL tools for more complex processing. Due to its popularity, fslmaths has evolved to support many of the most needed image processing functions of our field. Its widespread adoption is typified by the development of convenient wrappers that call this tool from other environments, such as the python-based nipype.3 Beyond describing the functions and idiosyncrasies of fslmaths, we introduce the niimath clone, which can provide benefits with regards to licensing, performance and portability. In particular, we showcase how niimath can be embedded into web pages and the ‘imbibe’ R package.
The fslmaths tool offers a rich set of capabilities, including image masking, thresholding, and mathematical operations on brain images, making it an essential tool for many researchers in the neuroimaging community. While fslmaths can be called directly from the command line, it also provides core functionality for many of the popular higher-level FSL1 pipelines including BET (Brain Extraction Tool), FDT (FMRIB’s Diffusion Toolbox), SIENA (analysis of brain change), TBSS (Tract-Based Spatial Statistics), FLIRT (FMRIB’s Linear Image Registration Tool), BASIL (Bayesian Inference for Arterial Spin Labeling MRI), VERBENA (Vascular Model Based Perfusion Quantification for DSC-MRI), FUGUE (FMRIB’s Utility for Geometric Unwarping of EPIs), FEAT (FMRI Expert Analysis Tool), POSSUM (Physics-Oriented Simulated Scanner for Understanding MRI), FIRST (model-based segmentation), and MELODIC ( Multivariate Exploratory Linear Optimized Decomposition into Independent Components). Therefore, improving and understanding fslmaths can have a direct impact on the usage of these popular pipelines. Given the need for general purpose mathematical operations that can be applied to the domain specific neuroimaging formats, it is unsurprising that each popular software package has developed their own image processing tool with many shared features. For example, consider the need to create a binarized mask image where voxels with an intensity greater than or equal to 80 are set to one and those below are set to zero with a NIfTI image named t1.nii (with FSL, one could use the command “fslmaths t1 -thr 80 -bin binT1”). AFNI4 users can apply 3dCalc (“3dCalc -a t1.nii -expr 'step((a - 80))' -prefix binT1.nii”). ITK-SNAP5 users have the c3d and c4d tools (“c3d t1.nii -threshold -inf 80 0 1 -o binT1.nii”). FreeSurfer6 users have several command line tools (“mri_binarize –i t1.nii –o binT1.nii –min 80”). SPM7 users can call imcalc to apply Matlab equations (“imcalc (i1\>80)”). For scientists who use Python, nibabel8 can leverage numpy optimized functions (“img = np.where(img > 80, 1.0, 0.0)”). While each of these tools provides redundant functions to each other, each has been adapted to the needs and file formats of its ecosystem. Indeed, many scientists and pipelines will use a combination of these tools best suited for different operations. For example, fMRIPrep9 combines AFNI, FSL, FreeSurfer, and Python. The fact that each core package has developed its own image mathematics solution reflects the core need for these functions across the domain.
Innovation10 and novelty11 are heavily weighted for scientific funding and high impact publications. Therefore, the incentive to develop clones (that replicate functionality but not internal code) needs justification.
Complex multi-function tools like fslmaths grow organically to fit the emergent needs of software development. The primary pressure is to robustly solve a problem, and concerns regarding performance and library dependencies are typically not a leading concern. A benefit of cloning a popular and mature tool is that one can understand the full scope of the project, identify optimizations, and remove dependencies. As we demonstrate later, niimath leveraged these aspects to create a smaller, faster and more portable tool that could be embedded into new niches. Indeed, a clone that uses a permissive and open license has the opportunity to showcase optimized routines that can be adopted by the cloned source. Below we describe how the development of FSL has been improved by including code from niimath.
Another potential benefit for developing a clone is to improve portability and to support additional platforms. The FSL tools are written in C++ and are portable across UNIX platforms, currently supporting both ARM and x86 architectures as well as both the Linux and MacOS desktop operating systems. However, officially FSL only runs on the Windows operating system via the Windows Subsystem for Linux. As we describe later, the portable design of niimath allows it to support multiple architectures, and operating systems including Windows, Linux and MacOS. Further, it can be provided as a compiled R package (‘imbibe’) and compiled to Web Assembly, allowing it to be embedded into web pages regardless of hardware or operating system (e.g. extending support to tablets, phones and web-based applications).
A further benefit for cloning popular but complex software is to provide insight into its behavior. This can identify situations where the operation is not intuitive, not as described in the manual, or operates in unexpected ways for edge cases. This is particularly important for popular tools that do not adopt FOSS licenses, which can be a barrier to code inspection for some and thus reduce insights into the fundamental behavior of a tool.
Therefore, we argue that niimath substantively contributes to fslmaths and the wider neuroimaging community by addressing remaining gaps in licensing, performance and portability of fslmaths. In addition, a clone can provide insight into the behavior of popular but complex tools and the discoveries made during reimplementation can be back-ported, improving the original software. Subsequent sections describe how niimath successfully delivers all of these benefits.
Methods / Implementation
Design Considerations
The vision for niimath was to develop a clone of fslmaths that would be open, fast, portable, and have minimal dependencies. We chose the C language for its widespread support and relatively good compiler optimization support. The first stage was to evaluate whether modern architectures and compilers benefit from hand tuned code. In general, we found few benefits for using hand-tuned vectorized instructions (https://github.com/neurolabusc/simd), perhaps suggesting that well designed algorithms tend to be limited by memory bandwidth, modern compilers can auto-vectorize simple routines, and that memory bandwidth compounded by file input/output pose a bottleneck for rapid routines. The final niimath code includes a few Single Instruction/Multiple Data functions for the x86 and ARM architectures (these are enabled with the SIMD compiler directive, so they are automatically disabled for situations where they are not supported, such as for WebAssembly).
License
One notable reason to clone a successful product is to provide a less restrictive license. For example, the popular Octave language is a clone of the professional MATLAB12 while the R language drew inspiration from the proprietary S.13 Free and open source software (FOSS) can aid research.14 While FSL is free for noncommercial use, the copyright does place some restrictions on the usage, in particular for commercial exploitation. This license provides source-available software that is free for academic research but can create barriers for developers of other software tools as they may avoid inspecting the FSL routines, as intentional or unintentional transference of code could jeopardize their own licenses. This aspect can restrict the ability of other teams to contribute to FSL, as these may conflict with the way that their home institution handles intellectual property. On the other end of the spectrum, the popular SPM7 uses the open but restrictive copyleft of the GNU General Public License (GPL). GPL code can only be embedded in open software that adopts the GPL. Therefore, any software that wishes to include GPL code must be free and open. The GPL can therefore suffer from the same issues with code commercialization, inspection and contributions. While we respect and understand the choices behind the FSL and SPM licenses, we suggest that the permissive and open BSD 2-Clause License used by niimath has clear benefits when possible. This license allows developers to inspect, extend and embed this software into their own packages, regardless of their preferred license (as long as they retain the original copyright for the specific code and acknowledge the original authors are not responsible for any damages). For example, this license is used by our popular dcm2niix15 which has allowed it to be included with the institutional licenses used by FSL,1 FreeSurfer,6 several commercial products, and numerous open source projects including Dcm2Bids16 which uses the GPL. Likewise, the dcm2niix Github repository documents many contributions from industry, including engineers at the major MRI scanner manufacturers GE, Mediso, Philips, Siemens, and UIH. We see permissive open source licenses as an opportunity to leverage community-driven development, permitting individual researchers with unique insights into neuroimaging analysis within their specific domains to collaborate, innovate, and contribute to the advancement of the field through new tools that fill different niches than the original software, all while respecting their own preferences and licensing requirements. From this perspective, permissive open source software are the universal donors, analogous to the O negative blood type. The class of permissive open source licenses include the Apache, MIT and BSD licenses (though note that the Apache License is distinguished by an additional patent grant clause). While all three are compatible with the GPL, the BSD 2-Clause License is considered the most permissive and allows for integration with a wider range of projects.
Installation
We share niimath via a github repository (https://github.com/rordenlab/niimath) that includes the source code as well as compiled releases of each major version. The repository describes how to compile niimath using the cmake, make and msbuild wrappers to invoke the clang/LLVM, gcc or MSVC compiler. Each code update of the repository invokes an automatic compilation that generates Linux, MacOS and Windows compatible executables, and the Linux executables are automatically validated using the canonical_test script described in the Evaluation section, providing continuous integration and continuous deployment (CI/CD).
Evaluation
We created bash scripts designed to compare both the speed and validate the results of fslmaths-compatible tools. We provide all these scripts in a Github repository (https://github.com/rordenlab/niimath_tests) that allows others to replicate our results and also allows regression testing for future software tools. This repository contains 63 input images in the In folder that demonstrate edge cases: all 48 combinations for losslessly re-orienting the left-right, anterior-posterior and inferior-superior dimensions, images with both odd and even dimensions (e.g. to validate median solutions), images with non-finite voxel intensities (positive infinity, negative infinity, and not-a-number), binary images, plausible 4D timeseries (a short resting state dataset), and statistical maps. These input images were converted to 163 images in the Canonical folder using the included script canonical_make leveraging the release version of fslmaths 6.0.7.8 compiled for the ARM64 architecture of MacOS (13.6). These 163 derived images demonstrate the full range of fslmaths functions. The included script canonical_test can be used to validate the performance of any fslmaths compatible executable against these 159 images, to validate the accuracy of performance. By providing pre-computed validation images, we can detect differences between implementations and across different architectures. To enable evaluation, we added the novel function compare to niimath, which evaluates two images (e.g. a canonical reference image and a test sample) and reports if any voxel intensities differ. When images differ, a number of diagnostics are provided (location, intensity and difference of most divergent voxel; proportion of identical voxels, correlation of the two images, mean and standard deviation for each image). This function terminates with an error if the absolute maximum difference between fslmaths implementations exceeds a user specified threshold. This allows automated regression tests that tolerate a little variation for functions where variation is expected, while detecting gross errors. We describe the rationale for this tolerance next.
The need for reproducible results in neuroimaging is critical17 and requires getting consistent results. However, it is worth emphasizing that a neuroimaging tool can provide slightly different results in different environments.18 Neuroimaging computations are conducted using floating point representations, where the precise order of instructions, subtle assumptions of those instructions and precision of each instruction can generate small rounding differences. As Kernighan and Plauger note19 “Floating point numbers are like piles of sand; every time you move one you lose a little sand and pick up a little dirt”. For example, the same version of FSL can generate numerically different results on different installations.18 This can reflect different hardware (ARM vs x86 CPU), different instructions (e.g. a fused multiply–add instruction reduces the rounding error of computing two separate instructions), different co-processor (e.g. a x86 FPU instruction uses 80-bits internally, while a SSE instruction on the same machine uses 64-bits), different optimizations (e.g compiler --ffast-math flag), and different versions of the dependent library. Likewise, different algorithms or precision for computing the same mathematical function can generate slightly different results. For example, fslmaths applies a Gaussian blur with a kernel size that is 6.0 times the sigma, while the AFNI default is 2.5 (AFNI_BLUR_FIRFAC). While these variations tend to be negligible in magnitude, it does make reverse engineering tools challenging as validation tests must distinguish whether variations are meaningful. Likewise, end users must set realistic expectations regarding equivalent versus identical results. Therefore, while niimath and fslmaths generate results that are not always identical, the results are intended to be always comparable. To aid this, niimath includes a novel function --compare that compares two images and identifies the magnitude and location of the most discordant voxel.
By design, the previously described validation scripts are designed to be unusual to elicit anomalous behavior and small to aid CI/CD. To provide a realistic evaluation of the speed of different implementations, we also provide the script slow_benchmark.sh that tests the time to perform different operations on realistic datasets. These larger datasets are available from a separate repository (https://osf.io/y84gq/) and were acquired on a 3T Siemens Prisma MRI scanner using the Human Connectome Project protocols20 (specifically, a 4D resting-state time series and a 3D T1-weighted anatomical scan).
Results
As expected and previously noted,21 our validation tests detect that the same version of fslmaths will generate slightly different results on different architectures and operating systems. In all cases the observed differences were negligible. We first compared fslmaths to itself, comparing the canonical images created on a MacOS computer using fslmaths compiled for the ARM architecture to the same code compiled for a x86-64-based Linux computer. Four of the 159 tests generated some variation: fmean (maximum difference 1.90735e-06), fmeanu (1.90735e-06), bptf high-pass (1.81899e-12) and bptf band-pass (4.9738e-13). We next compared fslmaths to niimath for the same architecture (MacOS ARM64). Four of the 159 tests generated some variation: bptf high-pass (1.90735e-06) and bptf band-pass (1.04904e-05). Finally, we compared across tools and architectures by comparing the results from the ARM64 MacOS fslmaths to the x86-64 Linux niimath. Here, the results were identical with exception of the same four of the 159 tests that differed when comparing fslmaths to itself across architectures: fmean (1.90735e-06) fmeanu (1.90735e-06), bptf high-pass (1.90735e-06) and bptf band-pass (1.04904e-05). The results of the fmean and fmeanu functions are architecture dependent, such that fslmaths and niimath produce identical results on the same architecture. Across all of these divergent tests, the vast majority (always over 98%) of voxels were numerically identical across methods. These tests suggest that while variation across implementations and architectures exist, the magnitude of variability is negligible.
While niimath typically generates equivalent results to fslmaths, we did discover some unexpected behavior with fslmaths 6.0.7.2, and a few differences were notable:
-
The command “
fslmaths inputimg -add 0 outputimg -odt input” can convert integer images (e.g. uint8 datatypes) to float output despite explicit request to retain input type. This occurs if the input image header has a non-unitary scale slope or non-zero intercept: in these cases FSL interprets the fundamental type to be float. In contrast, niimath retains both the datatype and the intensity scaling parameters when this is explicitly requested (both fslmaths and niimath return float data if the output data type is not specified). Furthermore, different versions of fslmaths perform differently for the pass through “fslmaths in out” which is useful for copying files. Old versions will losslessly save in the input datatype, while fslmaths 6.0 and later converts the data to float. niimath retains the original datatype. While these two situations may seem like an unusual edge cases, these calls provide a simple way to clone an image. Alternatively, FSL does provide its immv and imcp commands for these purposes. -
In developing niimath we discovered a bug in the then current versions of fslmaths, which were unable to process files where the string “.nii” appears in a folder name.
-
The fslmaths “
-dilD” function formodal dilationdid not consistently insert a modal value, often inserting the maximum value it observed in the kernel. The latest version of fslmaths (6.0.*) now correctly calculates the mode, in issues of ties the tied value with the maximum intensity is used. -
The fslmaths “
-roc” receiver operating characteristic implementation explicitly ignores the (5-voxel wide) boundary of an image. Therefore, it ignores voxels near the edge of an image and generates the error “given object has non-finite elements” if any dimension is less than 12 voxels. -
The upper and lower threshold -thr or -uthr functions expect numbers rather than images but, like other functions in fslmaths it, will appear to run if the input is an image, implicitly treating it is a zero value without properly throwing an error..
-
Perhaps understandably, asking for the remainder when dividing by zero (“
fslmaths in1 -rem 0 out”) will crash without an explanation. However, “fslmaths in1 -rem in2 out” will also crash without explanation if any voxel in the image in2 is zero. In contrast, niimath provides a divide-by-zero warning message describing the reason that the operation failed. -
The fslmaths function -rem uses the C language convention of the
%operator, and returns the integer modulus remainder even though it generates floating point images as default. This may be unexpected for users of other languages, e.g. in Python “2.7 % 2” is 0.7, just like MATLAB’s “mod(2.7, 2)”. niimath clones the fslmaths behavior, but also includes a new function -mod to return the modulus fractional remainder. -
FSL does not use NIfTI voxel coordinate conventions internally but aims to have all input and output coordinates in user interfaces use NifTI conventions. However, the fslmaths -tfceS option does not correctly use the NIfTI convention in this specific case (fixed in fslmaths 6.0.7.7+).
-
Neither downsampling with the -subsamp2 nor -subsamp2offc functions in fslmaths accounts for anti-aliasing. Be aware that -subsamp2offc can exhibit odd edge effects. The problem is simple to describe. Intuitively, for slices in the middle of a volume, the output slice is weighted 50% with the center slice, and 25% for the slice below and the slice above. However, for bottom slices (as well as first rows, first columns, last rows, last columns, last slices) the filter weights 75% on the central slice and just 25% on the slice above it. Signal from this 2nd slice is heavily diluted. One potentially better mixture would be 66% edge slice and 33% 2nd slice. This latter solution is implemented in niimath. In addition, niimath introduces the novel function
-resizethat resamples data with anti-aliasing using the nearest neighbor, trilinear, spline, Lanczos or Mitchell filters as described by Schumacher.22 -
The fslmaths function -ztop for converting z-statistics to uncorrected p-values does not use the convention of clamping extreme values. Therefore it will report a p-value of precisely 1.0 for z values above 8 and precisely 0.0 for values less than -8. Likewise, -ptoz does not clamp values so (infinite) p-values of 0 and 1 will be converted to zero. niimath clones this behavior, but also provides clamped variations of these functions (-ztopc -ptozc).
-
We also note differences in the
rankandranknormfunctions where ties are given different values between niimath and fslmaths (e.g. when two voxels all have the same intensity and this is the brightest intensity in the image, the order that1,2is assigned depends on sorting algorithm). This reflects an ambiguous situation and both tools do not attempt to provide mean ranks (e.g. assigned the tied brightest voxels both the value1.5).
Further, niimath provides a few mathematical functions not found in fslmaths, filling gaps of the current FSL package (e.g. unsharp mask edge enhancement, sobel edge gradient enhancement, and the previously described resize functions). It also uses (with permission) code from AFNI’s 3d Teig software4 for diffusion tensor decomposition, leveraging these public-domain functions from AFNI (older portions use the GPL).
With regards to performance, the Human Connectome Project dataset demonstrates that niimath dramatically accelerates a range of operations (Table 1). This establishes that niimath is substantially faster than fslmaths for many routines while generating equivalent results.
Modern neuroimaging pipelines tend to have multiple tools, each which loads image data, calculates a transformation and subsequently saves a new image. As computers have become faster at computation, the speed of loading and saving data becomes significant. These effects can become amplified on server and cloud instances, where file reading and writing can be relatively slow. Tools like FSL often compress NIfTI images using the GZip format, which reduces disk size, though the decompression and in particular compression can be slow. We developed niimath to be able to use four different methods of GZip compression: an inbuilt miniz library (https://github.com/richgel999/miniz), the zlib installed on the computer (system), the parallel pigz which can leverage multiple threads, or the CloudFlare zlib (https://github.com/cloudflare/zlib). We noted that the CloudFlare library is twice as fast as the system zlib (https://github.com/neurolabusc/zlib-bench-python).
Discussion
Our evaluation demonstrates that fslmaths and niimath generate equivalent results. The adage “imitation is the highest form of flattery” is widely recognized. In the course of time, our discipline has identified a handful of essential tools that serve as the bedrock of our research. From first principles, these core tools have become popular because they fill critical needs. Typically, over time these features have further evolved to address the core needs of the community. We contend that there is merit in revisiting, enhancing, and gaining a deeper comprehension of these fundamental tools. Our field invests significant financial and energy resources in data processing, and enhancing the core tools can yield valuable dividends for the entire community. Beyond improving performance, these enhanced tools can fit emerging niches, such as cloud edge computing and the R scripting language.
Improving FSL
We recognize that most FSL users will continue to prefer the proven fslmaths over niimath when using the established FSL pipelines. As described above, the latest release of fslmaths has already adopted changes based on our discoveries of unexpected behavior. Furthermore, our work identified several key optimizations that have been introduced in recent versions of FSL, contributing to its improvement. First, FSL is now distributed with the CloudFlare zlib (to facilitate this we replaced a GPL function with a permissive equivalent to allow inclusion into FSL). This doubles the speed of most image reading and writing operations. Furthermore, we noted that the FSL tool distancemap and equivalent AFNI functions were exceptionally slow at computing the Euclidean Distance Transform (EDT). These tools were calculating this function in 3D, whereas the problem is separable and can be computed as three 1D functions.23 For some typical images, this accelerated the processing time from 36.46 hours to just 1.5 seconds (https://github.com/neurolabusc/distancemap). This method has now been incorporated into FSL’s distancemap, benefiting users of the popular Bianca24 and TBSS25 tools. Finally, many of the niimath/fslmaths differences reported above have been addressed by the FSL team, including -tfceS input coordinates, the -roc border, value checking for -thr* options, and improved help text for users. In all of these cases, the development of niimath has directly benefited the original tool.
Beyond the command line
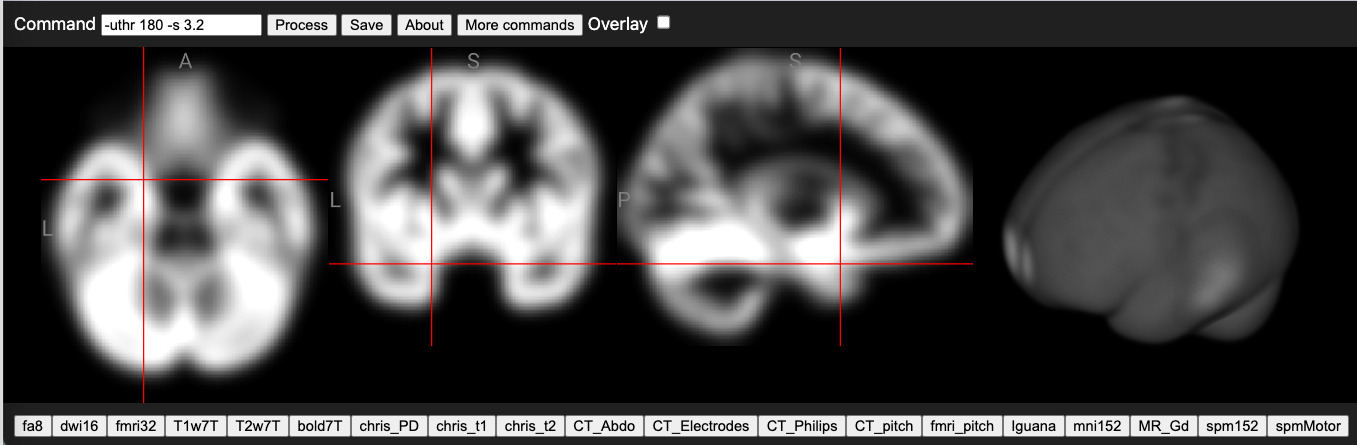
The niimath clone uses minimal dependencies, which allows it to be easily packaged in novel ways. One of our derivatives is imbibe, an image calculator that is provided as a package for R. This provides R users with a set of popular image processing routines, providing the performance of low-level optimized C code with the convenience of R scripting, and a pipe-based style of operation chaining familiar to R users through popular packages such as “dplyr” (https://dplyr.tidyverse.org/) for tabular data. A second novel application leverages the Emscripten LLVM-to-WebAssembly (WASM) compiler (https://github.com/emscripten-core/emscripten) allowing niimath functions to be directly called by JavaScript applications. JavaScript is an interpreted language with all numerics computed with double precision, resulting in slow performance.26 Therefore, niimath can provide the most popular image processing routines in our field, using a popular syntax, with high performance for easy access to cloud applications. This allows a zero-footprint web page to calculate complex image processing functions on the user’s computer. Since this computation happens locally, the user does not have to share their data across the web (this edge computing is important for privacy, in particular as neuroimaging data contains recognizable features). Relative to cloud computing, image data does not have to be uploaded to and downloaded from the cloud, avoiding the penalty for slow internet connections. Since the entire software is embedded in a web page, the user does not have to install any software and the routines work on any browser-compatible device (tablet, phone, computer) regardless of operating system. We envision these routines will enhance the capabilities of local machine learning based inference.27 For example, image processing routines can normalize data and do traditional image processing while machine learning can aid in the tissue segmentation, region of interest identification, lesion detection and detecting white matter hyperintensities. A live demo web page of niimath is available to demonstrate these features (Figure 1).
Resources and Support
The core niimath software is available on Github (https://github.com/rordenlab/niimath). The R wrapper imbibe has its own page (https://github.com/jonclayden/imbibe). Likewise, the WebAssembly implementation is hosted on Github (https://github.com/niivue/niivue-niimath) and has a live demo (https://niivue.github.io/niivue-niimath/) that provides a zero-footprint web page for exploring the capabilities using NiiVue28 for visualization. All of these projects exploit the Github mechanisms for reporting issues, forking the code and making novel contributions.
Acknowledgements
We recognize that fslmaths was developed organically and had contributions from numerous developers and the community to refine its capabilities. Tool development by CR is supported by NIH RF1-MH133701 and P50-DC014664. All research at Great Ormond Street Hospital NHS Foundation Trust and the UCL Great Ormond Street Institute of Child Health is made possible by the NIHR Great Ormond Street Hospital Biomedical Research Centre. We are grateful that the FSL team explicitly allowed us to copy the fslmaths command line help verbatim, providing users with a consistent interface regardless of the underlying code. We thank Benoît Béranger for improving niimath compilation. We are grateful to the AFNI developers for allowing us to re-use their tensor decomposition routines.
Conflict of Interest
MW and MJ receive royalties from Oxford University Innovations for licensing of the FSL software for commercial, non-academic use.